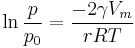Kelvin equation
The Kelvin equation describes the change in vapour pressure due to a curved liquid/vapor interface (meniscus) with radius  (for example, in a capillary or over a droplet). The Kelvin equation is used for determination of pore size distribution of a porous medium using adsorption porosimetry. The equation is named in honor of William Thomson, commonly known as "Lord Kelvin".
(for example, in a capillary or over a droplet). The Kelvin equation is used for determination of pore size distribution of a porous medium using adsorption porosimetry. The equation is named in honor of William Thomson, commonly known as "Lord Kelvin".
The Kelvin equation may be written in the form
where  is the actual vapour pressure,
is the actual vapour pressure, 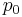 is the saturated vapour pressure,
is the saturated vapour pressure,  is the surface tension,
is the surface tension, 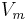 is the molar volume,
is the molar volume,  is the universal gas constant,
is the universal gas constant,  is the radius of the droplet, and
is the radius of the droplet, and  is temperature.
is temperature.
Equilibrium vapor pressure depends on droplet size. If 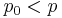 , then liquid evaporates from the droplets.
, then liquid evaporates from the droplets.
If 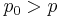 , then the gas condenses onto the droplets increasing their volumes.
, then the gas condenses onto the droplets increasing their volumes.
As  increases,
increases,  decreases and the droplets grow into bulk liquid.
decreases and the droplets grow into bulk liquid.
If we now cool the vapour, then  decreases, but so does
decreases, but so does 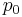 . This means
. This means 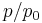 increases as the liquid is cooled. We can treat
increases as the liquid is cooled. We can treat  and
and  as approximately fixed, which means that the critical radius
as approximately fixed, which means that the critical radius  must also decrease. The further a vapour is supercooled, the smaller the critical radius becomes. Ultimately it gets as small as a few molecules and the liquid undergoes homogeneous nucleation and growth.
must also decrease. The further a vapour is supercooled, the smaller the critical radius becomes. Ultimately it gets as small as a few molecules and the liquid undergoes homogeneous nucleation and growth.
See also
References
- W. T. Thomson, Phil. Mag. 42, 448 (1871)
- S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, 2nd edition, Academic Press, New York, (1982) p.121
- Adamson and Gast, Physical Chemistry of Surfaces, 6th edition, (1997) p.54